誘電体とは、絶縁体であり、分極する物質です。絶縁体なので、電流を流さないような物質ですが、分極するという特徴を持っています。今回は、この誘電体の分極の微視的なイメージと巨視的なイメージについて説明します。
分極の微視的なイメージ
分極とは、電気的に中性の物質が、プラスの電荷を持つ物質とマイナスの電荷を持つ物質に分かれて、それぞれの電荷の中心が離れることです。
例として、ひとつの原子について考えます。原子は全体としては電気的に中性ですが、プラスの電気を帯びた原子核とマイナスの電気を帯びた電子から構成されています。この時点では、プラスの電気の中心(原子核の中心)と、マイナスの電気の中心(電子雲の中心)は一致しています。この原子に電場を与えると、電場から力を受けてそれぞれの電気の中心にズレが生じます。このとき、プラスの電気を持つ原子核は電場の方向へ、マイナスの電気を持つ電子は電場と逆の方向にわずかに動いて、それぞれの電荷の分布に偏りが生じます。しかし、それぞれの電荷を合計するとゼロになる。これが分極です。
マイナスの電気を帯びているのは電子である必要はありません。極性分子も分極します。もともと分子内に電荷の偏りがあるものを極性分子と呼びます。身近な極性分子には水があり、水の場合は酸素がマイナスの電気を帯びています。水の比誘電率は20℃で約80であり、アルミ電解コンデンサの誘電体である酸化アルミニウムの約8.5を大きく上回ります。
このような誘電体の分子レベルの挙動が、誘電体の巨視的な挙動を考えるうえで重要になっていきます。
電気双極子モーメント
誘電体の分極のように、ひとつの粒子の中でプラスの電荷とマイナスの電荷に分離し、それぞれの電荷の中心が無限小の間隔だけずれている状態を電気双極子と呼びます。電気的なふたつの極性がある原子(分子)、という意味ですね。
さて、この分極した電気双極子の状態を物理的に表すことができれば、誘電体の性質を詳しく見ていくことができるようになります。この状態を表すための物理量が、電気双極子モーメントで、次の式で定義されています。
\(\vec{p} = q \vec{d}\)
原子1個の場合を考えます。原子の電荷がゼロの状態から、正電荷\(+q\)と負電荷\(-q\)に分離し、このときの両電荷間の距離を\(d\)とします。負電荷から正電荷への向きを正とするベクトル\(\vec{d}\)と電荷\(q\)をかけたものが電気双極子モーメント\(\vec{p}\)です。
これで原子1個の電気双極子モーメントの物理量が求まりました。ここから、原子というミクロなレベルからマクロなレベルへ物理量を拡張し、誘電体の性質へと結びつけていきます。
分極の巨視的なイメージ
分極する原子の集合体である誘電体を電場の中に置くことを考えます。電場の中に置かれた状態の誘電体内部では、それぞれの原子が分極します。実際には原子一個一個は複雑な運動をしたり、状態が常に変化したりしているため、ミクロな状態の原子一個一個を区別して考えることは非現実的です。そこで、これらを空間的にも時間的にも平均を取って考えます。つまり、すべての原子が電場に沿ってきれいに分極すると考えるわけです。
さて、誘電体内部ですべての原子が分極すると、それぞれの原子のプラスの電荷は電場の方向へ、マイナスの電荷は電場と反対の方向へ向きます。ここでの電場の方向とは、電場のベクトルを矢印で書いた場合の、矢印の先の方向を指します。すると、誘電体内部では原子がきれいに整列しており、ある原子のプラスの電荷と隣の原子のマイナスの電荷が向き合うことになり、このふたつの電荷が打ち消し合って、この部分での電化の合計はゼロになります。誘電体内部はすべてこのような状態のため、誘電体内部の電荷は全体としてはゼロ、誘電体の表面(電場の方向と反対の方向の側面)にのみ電荷が生じます。このとき、電場の方向の側面にはプラスの電荷が、電場の方向と反対側の側面にはマイナスの電荷が分布します。分極した誘電体の模式図を下に示します。
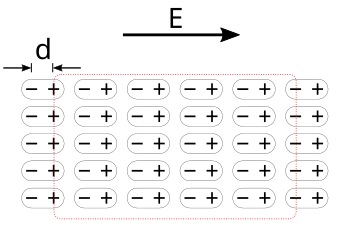
まとめ
誘電体は、まず原子レベルの挙動を理解することで、全体の挙動の理解につながっていきます。ここで述べた考え方をもとにして、分極と電場の関係へつなげていけるわけですが、この点については次回説明します。

コメント