コンデンサの用途_1ではパワエレ用途を説明しました。ここでは電力用途を説明します。
力率改善
力率は、交流電力を効率よく利用できているかどうかを示します。皮相電力に対する有効電力の割合で示されます。力率が最も優れているのが1、最も劣っているのが0で、通常はこの間の数値を取ります。なぜ力率を改善する必要があるかというと、一定以上の電力を消費する需要家(工場など)は力率が悪いと電気代が上がって、良いと下がるんですね。だから、こうした需要家は電気代を下げるために力率を改善しようとするんですね。力率が悪いところへコンデンサを適切に使用すると、力率が改善します。
そもそも電力とは?
名称に”力”が含まれていますが、物を押して動かす時の力(force)とは違います。英語での名称はelectrical powerです。powerは仕事率を指し、単位時間あたりに消費されるエネルギーを表す物理量です。電力の場合は、単位時間あたりの電流がする仕事で、電圧と電流の積で表されます。
直流の場合は電流も電圧も一定なので、電力は次のシンプルな式で計算できます。
\(P=VI\)
交流の場合は直流とは考え方を変える必要があります。以下では、電圧と電流がともに正弦波の場合について説明します。
交流は電圧と電流の大きさが時間とともに変化し、また変化の周期にズレがあったりするので、瞬間瞬間によって電流と電圧の積が変化します。
そこで、電圧の実効値を(\(V\))、電流の実効値をI、位相差を(\(\phi\))とすると、有効電力(\(P\))、無効電力(\(Q\))、皮相電力(\(S\))はそれぞれ次の式で計算できます。
\(P=VI\cos \phi\)
\(Q=VI\sin \phi\)
\(S=VI\)
これより、力率は次の式で計算します。
\(\dfrac{P}{S}=\dfrac{P}{\sqrt{P^{2}+Q^{2}}}\)
皮相電力とは?
直流と同じく、電圧と電流の積で表される電力です。皮相電力には有効電力と無効電力が含まれており、これらの比率が力率を決めることになります。
有効電力とは?
実際に工場の機械などを動かすのに利用される電力です。計算式に入っている\(cos \phi\)が力率です。電圧と電流の位相差\(\phi\)が小さい(ゼロに近い)と\(cos \phi\)は1(最大値)に近づき、位相差\(\phi\)が大きいと\(cos \phi\)はゼロに近づきます。つまり、位相差が大きいほど力率が低くなる(=悪くなる)ことがわかります。
無効電力とは?
有効電力と異なり、電力を使う機器に使われないけれども、送電線を通過するエネルギーです。位相差\(\phi\)が大きいと\(sin \phi\)は大きくなっていくので、無効電力も大きくなっていきます。ここからわかることは、同じ電圧と電流を流しても、力率が低いと有効電力が小さくなり、同時に無効電力が大きくなるということです。
位相差とは?
電圧と電流の波形の時間的なズレです。直流は電圧も電流も常に一定値を取るので、時間が変化してもずっと同じです。しかし、交流は電圧も電流も時間とともに変化し続けます。ただし、同じ変化を繰り返すので、数式や波形で表すことができます。この数式や波形を使って位相差を表すことができます。
電圧と電流を式で表してみます。電圧の最大値(波高値)を\(V\)、電流の最大値(波高値)を\(I\)、周期を\(T\)とした場合、時間\(t\)における電圧の瞬時値\(v(t)\)と電流の瞬時値\(i(t)\)は次の式で表されます。
\(v(t) = Vsin(\omega t)\)
\(i(t) = I sin(\omega t- \phi)\)
これを波形で表したのが下の図です。位相差がゼロのときは電圧と電流の波形の変化が同じ(ピーク値を取るタイミングが同じ)です。しかし、位相差がゼロではないときは、電圧と電流のピークを取るタイミングにズレがあるのがわかります。
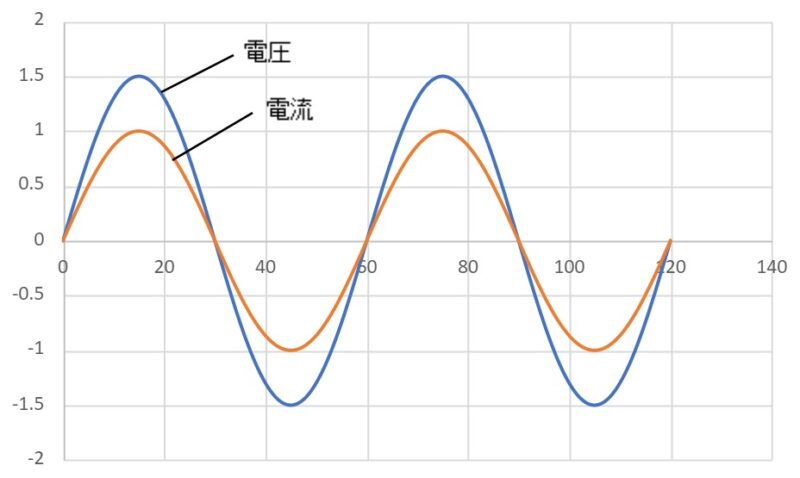
位相ゼロ
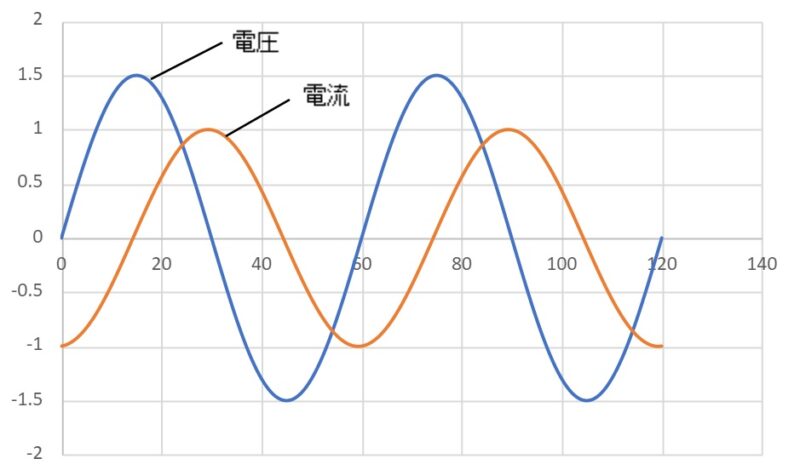
位相あり
これらの式には\(\omega\)が含まれています。この\(\omega\)は各周波数と呼ばれるもので、\(2 \pi /T\)で計算される数値です。\(sin0\)から\(sin2\pi\)で1周期を表すので、 \(2 \pi\) に\(t/T\)を掛けることで、1周期中の位置を示します。
この式では電圧波形を基準として、電流波形が電圧波形からどの程度ずれているかを\(\phi\)で表しています。
なぜ力率が低くなると良くないのか
それは、電気を使う人は消費した有効電力に対して電気料金を払うからです。無効電力が大きいと、実際に使う電力(有効電力)以上の電力を送電線に流す必要が出てくるので、送電線をより大電力に対応可能なものに変える必要が出てきて、お金がかかることになります。”無効”なものにお金をかけるのはもったいないですよね。そこで、電力会社は力率を改善すると電気料金を割り引く制度を設けています。逆に悪化すると割り増しされます。一般に、0.85以上を高力率、0.85未満を低力率と呼びます。なので、電力の需要家は、まずは力率0.85を改善の目安にすることになります。
なぜ力率は低くなるのか。
力率は電圧と電流の位相差によって決まります。電力を必要とする機器には誘導性負荷(モーターが代表格)が多いので、誘導性負荷の機器を多く使用すると交流電圧と交流電流の位相に差が生じ、力率が低くなっていきます。
力率の改善方法
力率改善用のコンデンサは毛色が少し変わっています。力率改善専用のコンデンサがあり、容量の表示力率改善用のコンデンサを使用すると、位相のズレをは毛色が少し変わっています。力率改善専用のコンデンサがあり、容量の表示が他の用途向けのコンデンサと異なります。コンデンサの容量というと、通常は静電容量を指し、単位はファラッド(\(F\))が使用されます。ところが、力率改善用コンデンサの容量はバール(\(var\))が使用されます。これは、容量が示す対象がまったく異なるからなんですね。
さて、力率の改善は、力率の現状を把握するところから始まります。パワーメーターという測定器で、簡単に力率を測定できることができます。たとえば、力率が0.8と測定されたとします。100kWの電力を使用する機器を使ってこの力率が出たとすると、100kW/0.8=125kVAが皮相電力です。力率が1なら皮相電力=有効電力=100kVAになるので、差し引き25kVAが無駄な電力分といえます。この25kVA分を、コンデンサを加えることでゼロに近づけるのが目標になります。一般的に、力率を1にするのは費用対効果が悪くなるので、95%ぐらいを目標にすることが多いようです。
さあ、どのようなコンデンサを使用すれば良いか?実は、簡単な早見表があります。改善前と改善後の力率が明確になったら、簡単に係数が求まります。それを先程の例での100kWに掛けることで、必要なコンデンサの容量(\(var\))が求まります。実際は、直列リアクトルを必要になりますが、趣旨から外れるのでここでは触れません。
ちなみに、容量の単位の\(var\)(バール)と\(F\)(ファラッド)は、お互いに次の式を用いて換算できます。
\(C=\dfrac{K\times 10^{9}}{2\times \pi \times f\times E}\)
ここで、\(C\)は静電容量(\(μF\))、\(K\)は力率改善用コンデンサの容量(\(kvar\))、\(f\)は周波数(\(Hz\))、\(E\)はコンデンサの定格電圧です。


コメント